Estimação Aumentada

Um pouco mais sobre o andamento da tese.

Depois da demora para obter alguns resultados, consegui hoje implementar uma sugestão de Canova e Sala (2009) para evitar o problema de falta de identificação dos parâmetros estruturais do modelo. O problema de identificação existe desde a estimação de sistemas de equações simultâneas, mas o desenvolvimento de modelos DSGE acabou mantendo a discussão ainda muito viva na academia. Para sintetizar, a ausência de linearidade dos parâmetros estruturais na solução dos modelos DSGE pode implicar na existência de diversos pontos de máximo na função-objetivo da estimação (a função de verossimilhança, por exemplo) e também na pouca curvatura da região em torno destes pontos de máximo, fazendo com que seja difícil localizar ("identificar") qual seria o máximo "verdadeiro" do modelo. A figura abaixo, tirada de uma nota que escrevi por aqui, talvez explique melhor o problema. No eixo vertical, o valor da verossimilhança do modelo é comparado com dois intervalos factíveis para dois dos parâmetros do modelo estimado na época.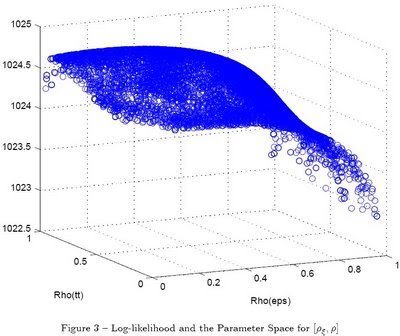


Notem como, para mudanças relativamente grandes do parâmetro Rho(eps), existe uma variação muito pequena entre os valores da verossimilhança em torno do máximo. Para ser mais específico, para valores de Rho(tt) próximos da unidade, um intervalo para Rho(eps) entre zero e 0.5 resulta em mudanças muito pequenas na verossimilhança do modelo.

Canova e Sala (2009) discutem este problema de forma mais detalhada, mostrando, inclusive, casos um tanto patológicos, onde parâmetros estruturais efetivamente desaparecem da solução do modelo, tornando a identificação destes parâmetros praticamente impossível. Na figura acima, seria o caso da função de verossimilhança ser um plano, com valores constantes da verossimilhança para todo o valor de Rho(eps), dado um valor para Rho(tt). Uma das soluções para o problema (discutida com maiores detalhes nas versões preliminares do paper) consiste em algo pouco intuitivo: se não for possível identificar um parâmetro, aumente o conjunto de parâmetros a serem estimados!!! Para ser mais exato, a inclusão de outros choques estruturais (e a consequente estimação dos seus parâmetros de persistência e variância) permite mais variação da função-objetivo em torno do valor "verdadeiro" dos parâmetros, facilitando o trabalho de identificação.

É curioso como o aumento do número de parâmetros pode servir para corrigir um problema de estimação. Na econometria clássica, o exemplo mais simples que posso pensar em uma situação destas é a autocorrelação residual por omissão de variável relevante: se estimamos um modelo de séries de tempo onde omitimos algum padrão relevante da análise, os resíduos serão correlacionados com o fator omitido. Assim, o acréscimo de um parâmetro e uma variável resolveria o problema. No caso apresentado aqui, é a inclusão de uma perturbação que permite ao econometrista obter informação relevante do modelo. É óbvio que nem toda perturbação resolve o problema de identificação (os choques adicionados devem ser relevantes na estrutura do modelo), como também é óbvio que esta não é a única solução disponível para o problema (leia o artigo e aprenda mais), mas a associação com o problema de econometria clássica me chamou muito a atenção.

A estimação que eu estava rodando parecia sofrer deste problema. Alguns fatores apontavam para isto: a pouca distância entre as médias das distribuição de priors e posteriors dos parâmetros (não é possível que eu seja tão bom a ponto de acertar o valor da grande maioria dos parâmetros do modelo); a convergência da distribuição dos parâmetros da posterior para a distribuição das priors (acertar não apenas na média, mas na distribuição é pior ainda!!!); a mudança dos valores da posterior dos parâmetros na mesma proporção em que mudo as priors.

O modelo tinha sete choques estruturais e dez choques de erros de medição ("measurement errors") das variáveis observáveis. Eu acrescentei mais quatro choques estruturais, e hoje terminei de estimar os valores modais da posterior. Na aparência, os valores dos parâmetros mostraram alguma mudança. Agora é esperar o computador terminar o trabalho braçal.

Volto para as leituras.

Abraços!